El decágono, la figura geométrica de 10 lados

La figura de 10 lados, en geometría plana, se llama decágono (deca = 10, como en “década”). En este artículo explicamos sus partes, tipos, y sus fórmulas de área y perímetro.

Antes de entrar en materia, aquí los links a otros polígonos similares, por si quieres echarles un ojo también:
Círculo · Triángulo · Cuadrado · Pentágono · Hexágono · Octágono · Decágono

Dicho lo cual, vamos allá!

Lados y Vértices del decágono

Los lados también se llaman “segmentos”. Están marcados en color morado en la imagen siguiente. Los vértices son las uniones entre dos segmentos, y están marcados con rojo. Como puedes contar en la imagen, el decágono tiene 10 vértices.

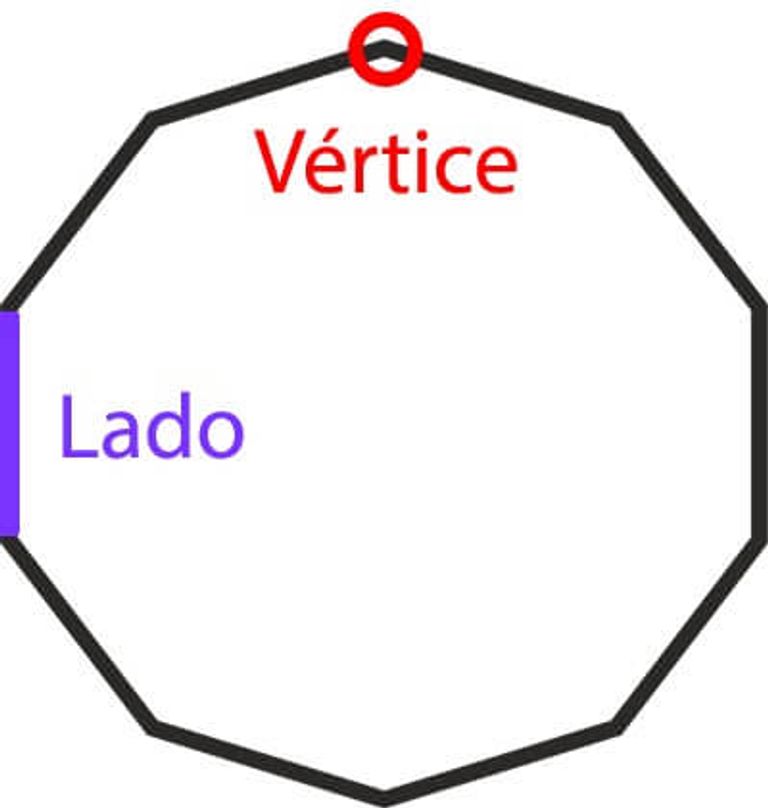
Si todos los lados miden lo mismo, hablamos de decágonos regulares. Si no es así (lagos desiguales), hablamos de decágonos irregulares.

Fórmula del Área del Decágono

Presentamos dos fórmulas para calcular el área de un decágono. La primera asume que se conoce la longitud de uno de los lados, la otra asume que adicionalmente se conoce la longitud de su apotema (no te asustes: más abajo explicamos qué es el apotema).

Fórmula del área conociendo la longitud de un Lado

Conociendo la longitud de uno de sus lados, podemos calcular el área de un decágono de la siguiente manera:

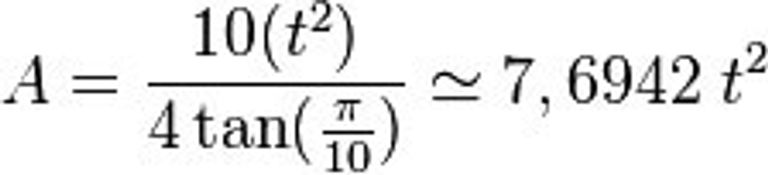
Donde:

A = área
10 = el número de lados
t = la longitud de cada lado
tan = la función tangente calculada en radianes

Fórmula del área conociendo la longitud de un Lado y el Apotema

Conociendo la longitud de uno de sus lados y también de su apotema, podemos calcular el área de la siguiente manera:

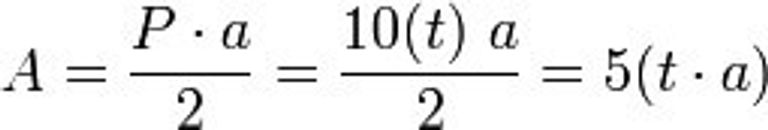
Donde:

A = área
P = perímetro
a = longitud apotema
10 = el número de lados
t = la longitud de cada lado

En esta imagen la misma fórmula se presenta de 3 maneras diferentes obteniendo en todos los casos la misma medida: el área de un decágono.

¿Qué es la apotema?

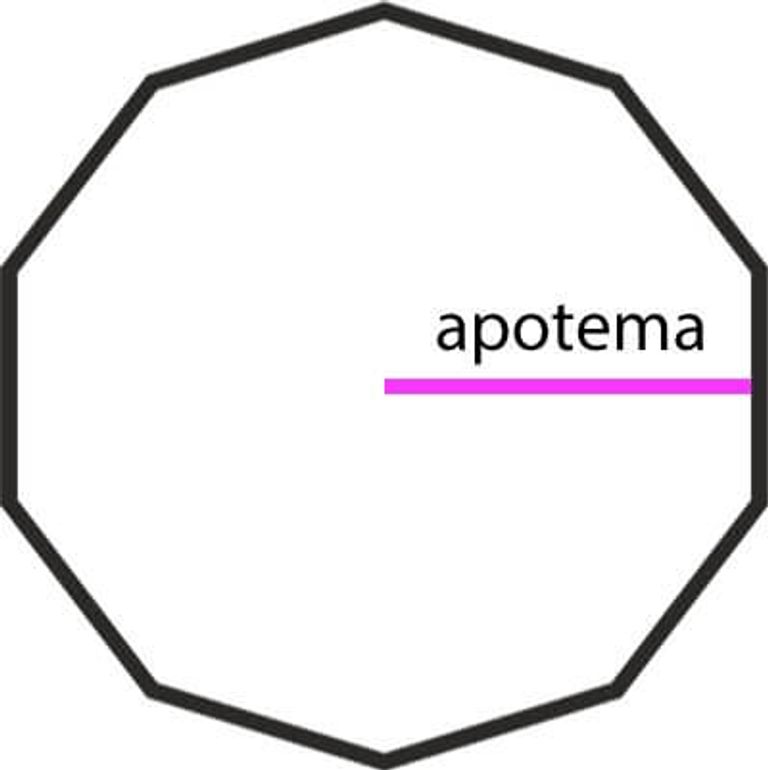
En el caso de un polígono regular como un decágono, el apotema (o la apotema, según el país) es la menor distancia entre el centro del decágono y cualquiera de sus lados. Para clarificar, observa la siguiente imagen. El apotema está marcada de color morado:

Fórmula del Perímetro del Decágono

Para calcular el perímetro de un decágono regular, simplemente seguimos la fórmula siguiente:

P = 10 * L

Donde:

P = perímetro
10 = el número de lados
L = la longitud de cada lado

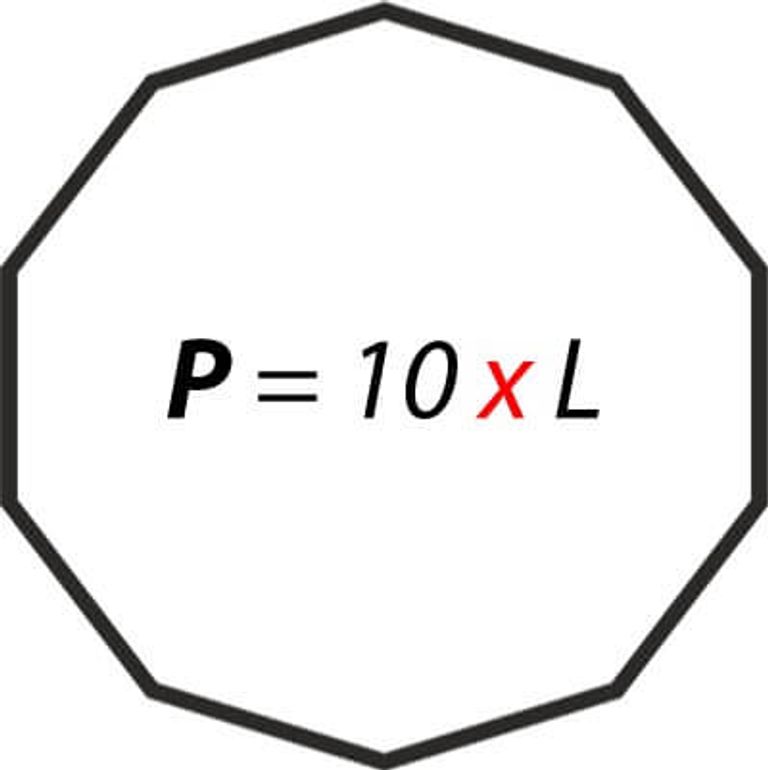
Cabe mencionar que dicha fórmula funciona para cualquier polígono regular. Simplemente cambiaría el número de lados, de forma que un pentágono por ejemplo, sería P = 5 * L.

Ángulos Internos

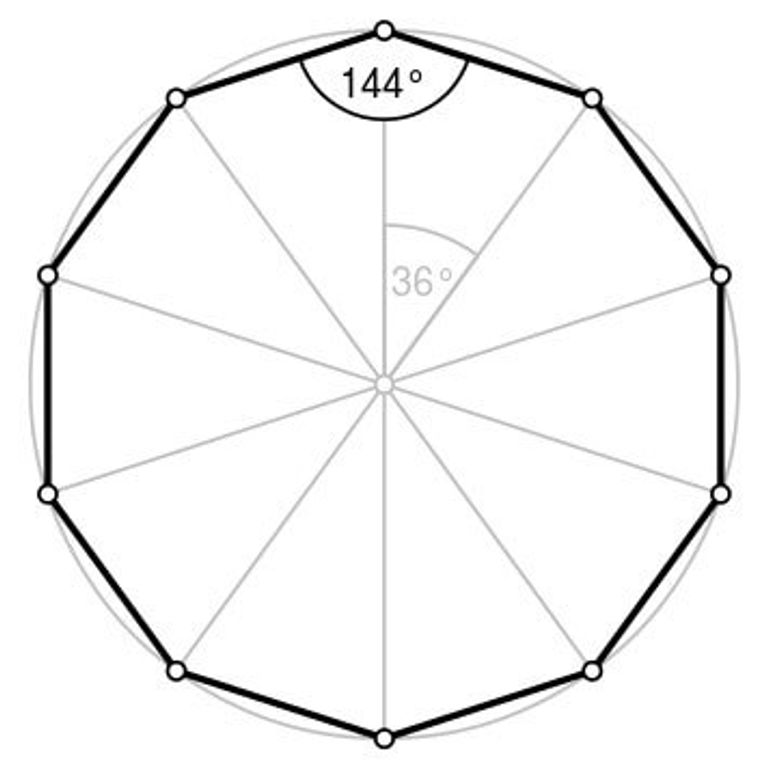
Un decágono regular tiene 10 ángulos internos de la misma graduación. Cada ángulo interno de un decágono mide 144°.

La suma de los 10 ángulos internos se obtiene multiplicando el número de lados (10) por la graduación interna (144), de forma que la suma de los 10 ángulos internos es 1,440 grados.

Ángulos Externos

Por otro lado, los ángulos externos miden 36° cada uno. De forma que los 10 ángulos externos suman 360° en total.

Decágono Regular

Un decágono regular tiene 10 lados con la misma longitud cada lado, y 10 ángulos con la misma graduación cada uno. En otras palabras, un decágono regular tiene lados y ángulos iguales. El resultado es una figura que se ve equilibrada y uniforme.

Decágono Irregular

Un decágono irregular es una figura plana de 10 lados con longitudes y ángulos desiguales. Esto significa que hay una enorme variación posible de combinación de longitudes y ángulos. Abajo hay un ejemplo:

Como se podrá observar, el número de decágonos irregulares posibles es virtualmente infinito.

¿Qué es una diagonal?

Una diagonal es una línea o segmento que une un vértice con otro dentro de una misma figura. Un decágono tiene en total 35 segmentos o diagonales. Las diagonales son de color turquesa en la siguiente foto.

Fórmula para calcular segmentos de un polígono

Existe una fórmula para lograr este objetivo. La fórmula es la siguiente:

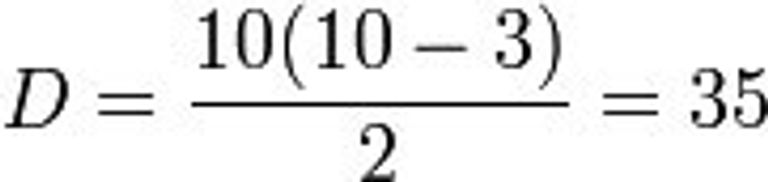
Donde:

D = diagonales
10 = el número de lados del polígono